关系模式

关系模式R(U)的一个分解p={Ri(Ui)}满足U=∪{Ui}，模式分解必须是无损连接并且需要保持函数依赖

无损连接

无损连接是指某关系模式的事例r按照关系模式分解成多个关系r1,…,rk，若r1,…,rk的自然连接（Join操作）等于r，则称该模式分解是无损的.

测试无损连接

Chase方法能够检测完全的无损连接，设有n个属性的模式R分解为k个模式Ri，有如下Chase过程：

1. 构造一个k行n列的表格，每行对应一个模式Ri，每列对应一个属性Aj，若Aj在模式Ri中则表格[i][j]中填入aj，否则填入bij
2. 扫描F中的每个FD X→Y
3. 若表格中有两行在X分量上相等，在Y分量上不相等则修改Y：若Y的分量中是个是aj，则另一个也修改为aj
4. 如果没有aj，则用其中一个bij替换另一个符号（i是所有b中最小的行数）
5. 重复2、3、4一直到表格不能修改为止
6. 若此时表格中有一行全是a，则该分解是无损连接的分解

当模式分解是简单的二元分解时（即p={R1,R2}），p是无损连接的分解当且仅当下面FD之一成立：

1. R1和R2两模式属性的交集 → R1与R2两模式属性的差集
2. R1和R2两模式属性的交集 → R2与R1两模式属性的差集

保持函数依赖

保持函数依赖是指关系模式R的FD集F在分解后仍在数据库模式中保持不变，这是模式分解的第二个条件

形式化的定义分解后F在模式Ri上的投影为：

πRi(F)={X→Y|X→Y∈F+⋂X、Y⊂Ri}

若分解p满足如下条件则称p\保持函数依赖\：

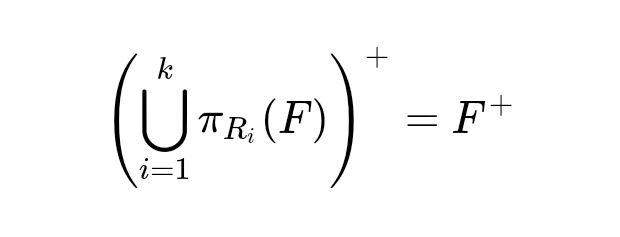
关系模式的范式

含义
范式xNF即是满足特定要求的模式，将低一级范式的关系模式通过模式分解转换为高一级范式的关系模式集合的过程叫做规范化

范式从低级到高级依次为：1NF、2NF、3NF、BCNF、4NF、5NF，高一级的范式总是低一级范式的真子集

根据关系模式R的不可约FD集F，可以画出节点是属性或属性集，边是由被依赖节点指向依赖节点的有向图来辅助分析关系模式，叫做函数依赖图

1NF

1NF要求关系模式R的每一个实例r均满足：r中的每一个元组t的每一个属性中只有一个值，这是关系模式的基本要求

不满足1NF的关系模式有二义性！

2NF

假定：R只有一个候选码，且该候选码为主码

R∈1NF且R的每一个非主属性（非候选码的其他属性）都完全函数依赖于主码时，R∈2NF

A完全依赖于W是指：W→A且A不依赖于任何一个W的真子集X，W是主键也可能包括多个属性{X、Y}，非主属性A不能局部函数依赖于X或Y

不满足2NF的关系模式可能存在［插入异常、删除异常、更新异常和数据冗余］，通过画出函数依赖图无损分解非2NF得到2NF，但2NF也不能完全消除上述问题

3NF

假定：R只有一个候选码，且该候选码为主码

R∈2NF且R的每一个非主属性都不传递依赖于主码时，R∈3NF
称A传递依赖于Y则有：Y→X，X→A，并且Y不依赖于X（即Y不等于X）、A不是X的子集

不满足3NF的关系模式也可能存在［插入异常、删除异常、更新异常和数据冗余］，通过打破传递依赖链条，把关系模式分解成多个子关系模式

BCNF

BCNF是3NF处理R有多个候选码的扩展，当R有多个候选码时即使R∈3NF，也可能出现［插入异常、删除异常、更新异常和数据冗余］，这时需要分解为BCNF范式

如果关系模式R的所有不平凡的、完全的函数依赖的决定因素（左边的属性集）都是候选码，则R∈BCNF
若要求保持函数依赖和无损联接，则总可以达到3NF，但不一定满足BCNF；因为BCNF可以达到无损连接，但不一定保持函数依赖

关系模式分解为范式的分解算法

保持函数依赖地分解R到3NF

算法步骤：
求出R的最小函数依赖集F

把所有不在F中出现的属性组成一个关系模式R’，并在U中去掉这些属性

若F中存在X→A且XA=U，则算法结束输出{R’,R(U)}，否则继续下一步

对F中的FD按相同的左部分组构成一个关系模式Ri(Ui)，Ui包括了该组FD涉及的所有属性

去掉{Ri(Ui)}中属性集Ui是其他某个关系模式属性集Uj子集的关系模式Ri，得到最终的分解p={R1,R2,…,Rk,R’}，p能够保持函数依赖地把R分解到3NF

无损连接且保持函数依赖地分解R到3NF

算法步骤：

按算法(1)中步骤求出保持函数依赖的3NF分解，设q={R1,R2,…,Rk}
设X是R的主码，p={R1,R2,…,Rk,R(X)}
若X是q中某个Ri(Ui)属性集Ui的子集，则删除p中的R(X)
输出p，p能够无损连接且保持函数依赖地把R分解到3NF

无损联接地分解R到BCNF